| Ch 10. Vibrations | Multimedia Engineering Dynamics | ||||||
| Free Vibs. Undamped | Free Vibs. Damped | Forced Vibration | Energy Method | ||||
| Free Vibrations- Undamped | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
A free-body diagram can be used to identify all the forces on a the platform. The weight, mg, will act on the spring but the spring force will counter-act the weight, so the weight actually cancels. The spring deflection will cause a force, ky, that will accelerate the platform. The final equation of motion becomes, The general solution of this differential equation is y(t) = A sinωnt + B cosωnt where ωn represents the natural frequency and is defined as |
|
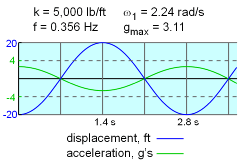
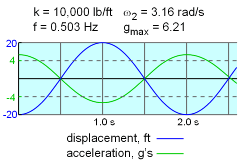
For the two cases, k1 = 5,000 and k2 = 10,000, the natural frequencies are found: case 1: ωn1 = 2.24 rad/s case 2: ωn2 = 3.16 rad/s The initial conditions for this particular situation are y(0) = -20 ft These two conditions can be used to determined the constants A and B. The final equation becomes y(t) = -20 cosωnt |
||
|
The velocity equation is determined by taking the time derivative of the displacement equation, dy/dt = -20 ωn sinωnt Likewise, the acceleration equation is found taking the second time derivative of the displacement, d2y/dt2 = -20 ωn2 cosωnt Therefore, the maximum acceleration is directly related to the square of the natural frequency, or This can be converted to g forces by dividing by the acceleration of gravity, gmax = 20/32.2 ωn2 = 0.621ωn2 g's The motion of the platform and its acceleration are plotted at the left for the two spring constants of 5,000 and 10,000 lb/ft. The 10,000 lb/ft case is unacceptable since the acceleration exceeds the safety limit of 4 g's. |
|