| Ch 5. Rigid Body General Motion | Multimedia Engineering Dynamics | ||||||
| Fixed Axis Rotation | Plane Motion Velocities | Zero Velocity Point | Plane Motion Accelerations |
Multiple Gears |
Rot. Coord. Velocities | Rot. Coord. Acceleration | |
| Rotating Coordinates: Acceleration | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
 Two Connected Bars |
Example |
|
|
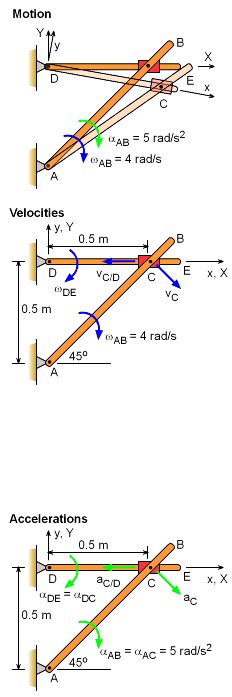
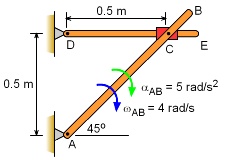
Two rods are pinned to a fixed point at one end, and connect to each other at the other end using a slider joint. Point C can freely move along rod DE but is pinned to rod AB at C. Rod AB rotates clockwise with angular velocity ωAB = 4 rad/s and angular acceleration αAB = 5 rad/s2 when θ = 45o. Find the angular acceleration of rod DE at this instant. The collar at C is pin connected to AB and slides over rod DE. |
||
| Solution |
||
|
|
Since the distance between point D and C varies, two frames of reference is useful to solve the problem. Attach the local x-y coordinate to the rotating AE rod, and the global X-Y coordinate to the non-moving background. Velocities: Putting all terms together gives, Acceleration of C can be determined from bar AC Putting all terms together gives, Comparing the j terms αDC = 11k rad/s2 (counter-clockwise) |
|
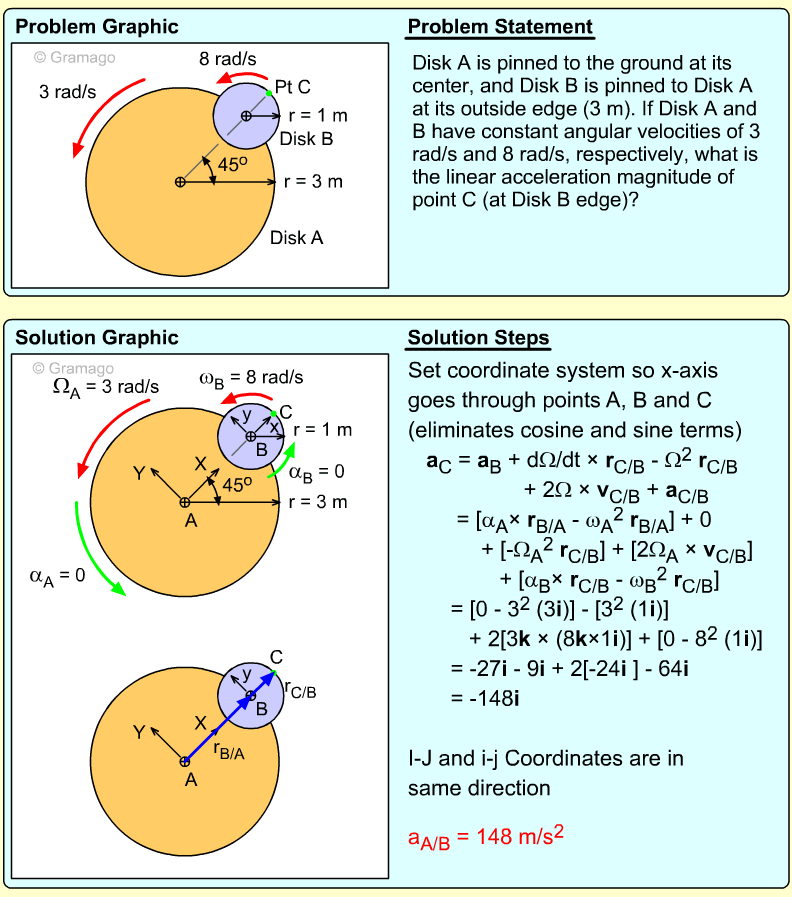
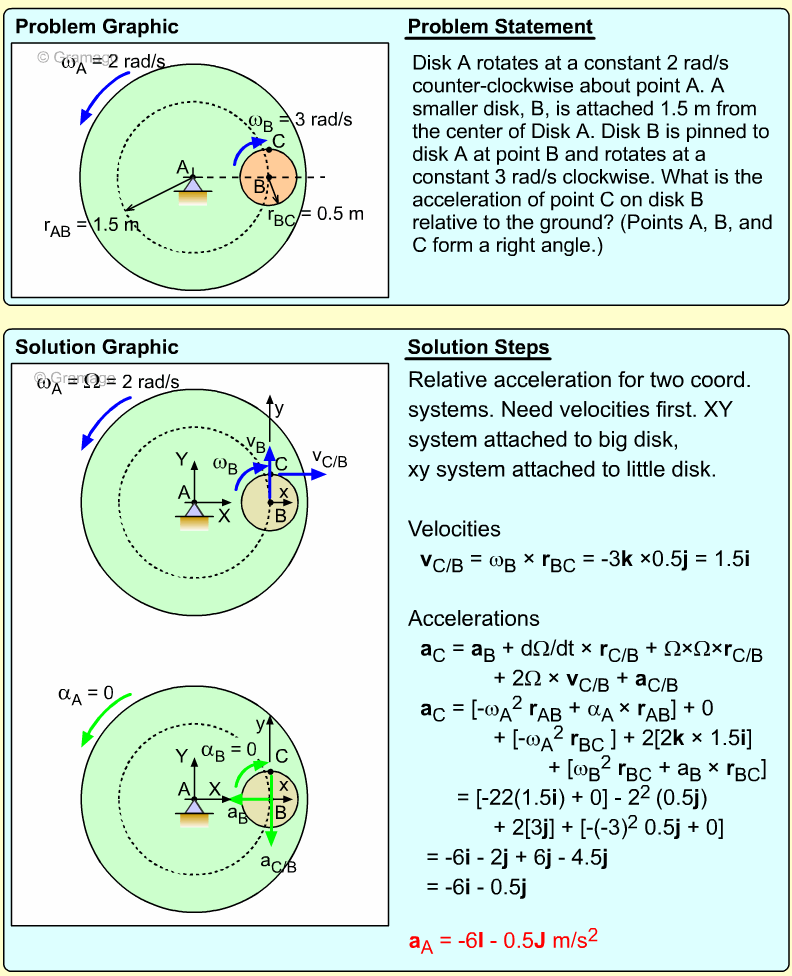
| Example Problem 1 |
||
|
||
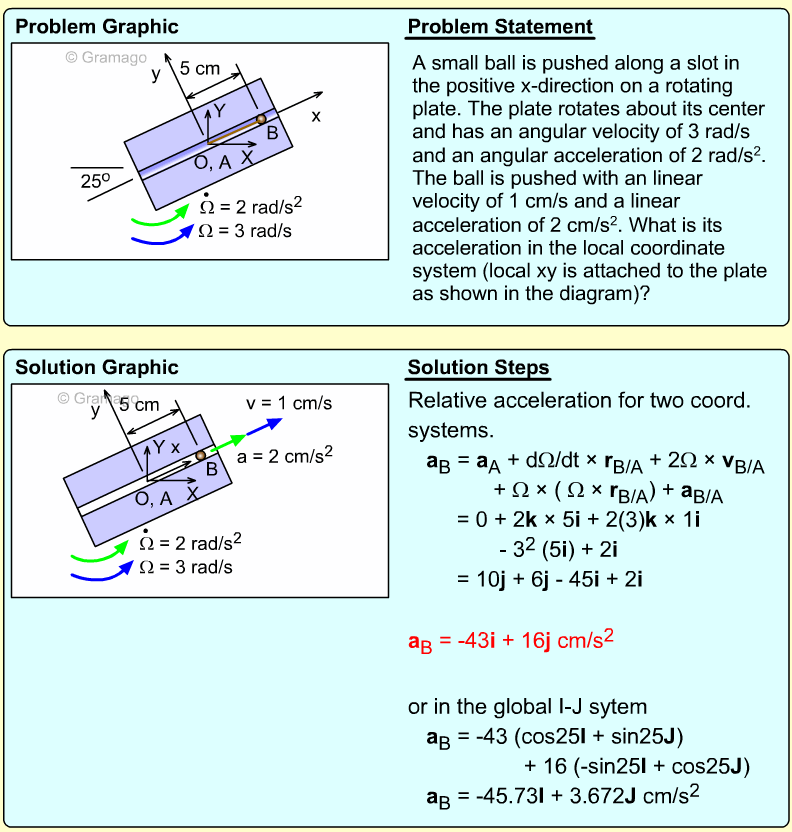
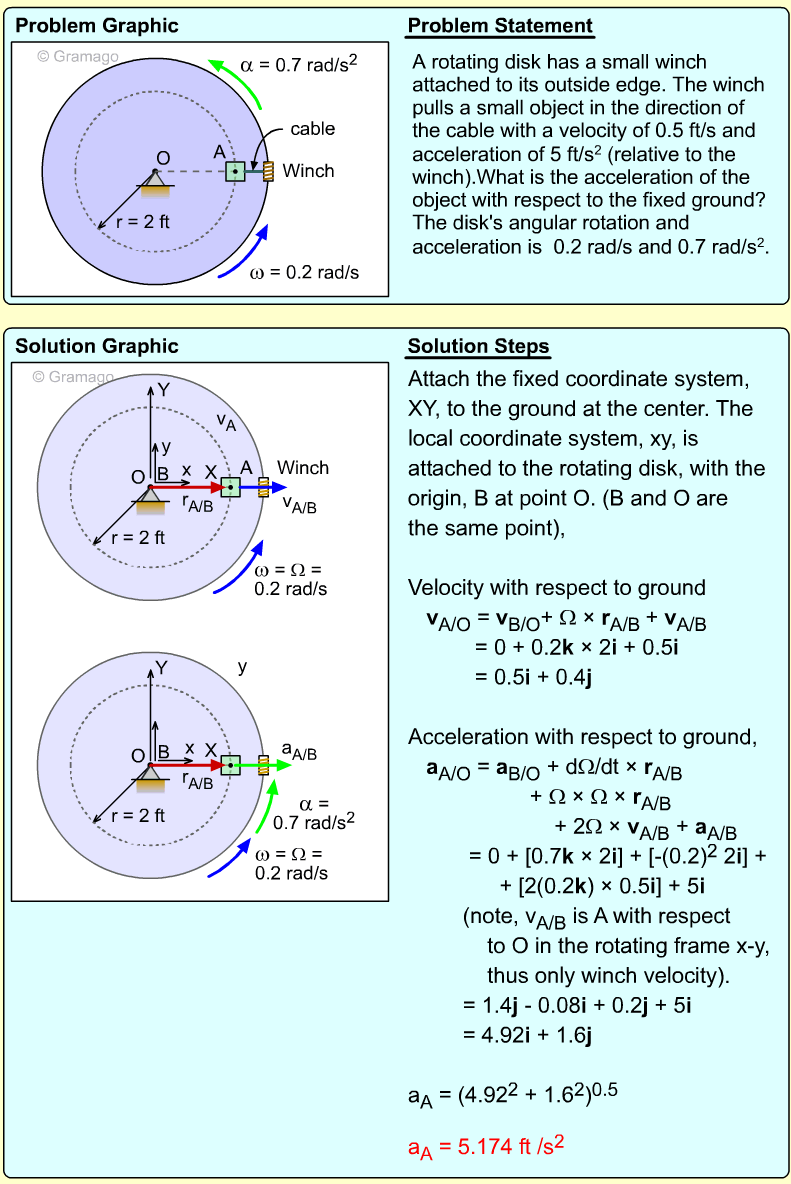
| Example Problem 2 |
||
|
||
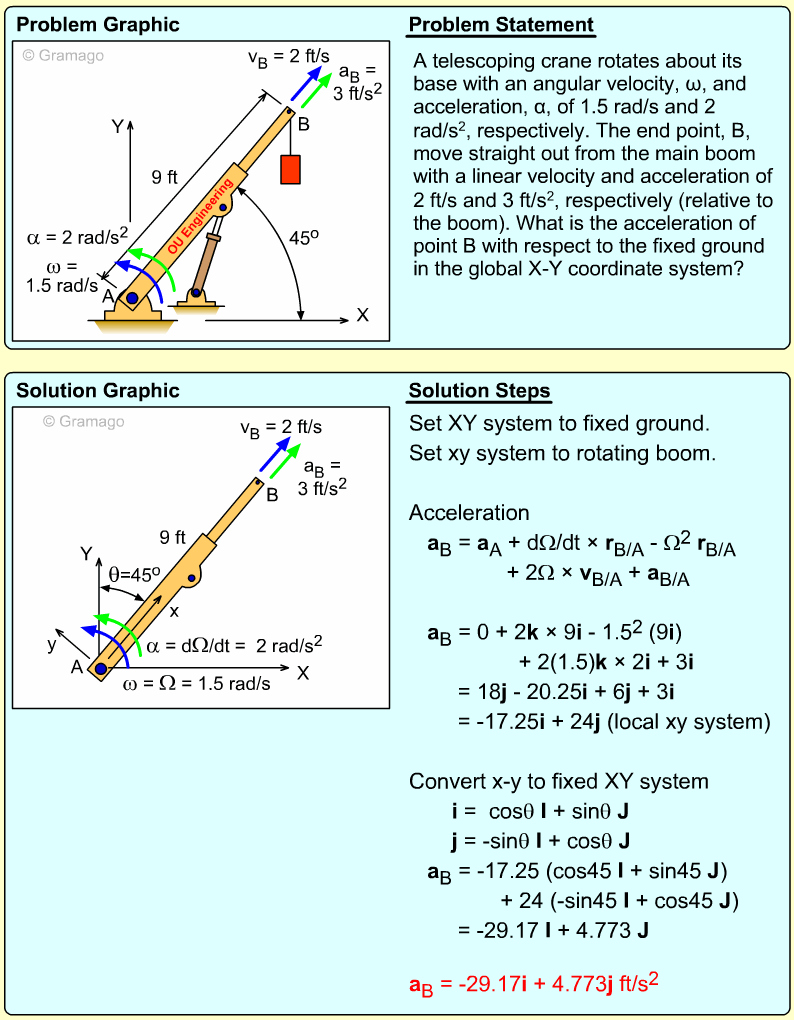
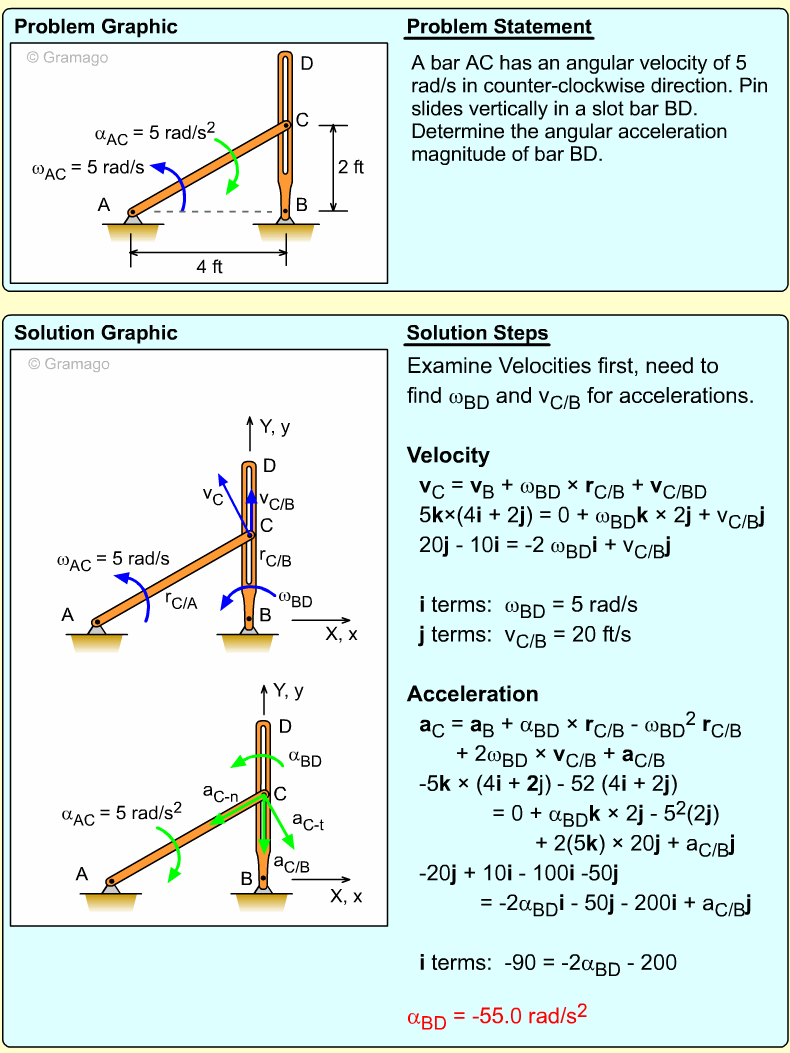
| Example Problem 3 |
||
|
||
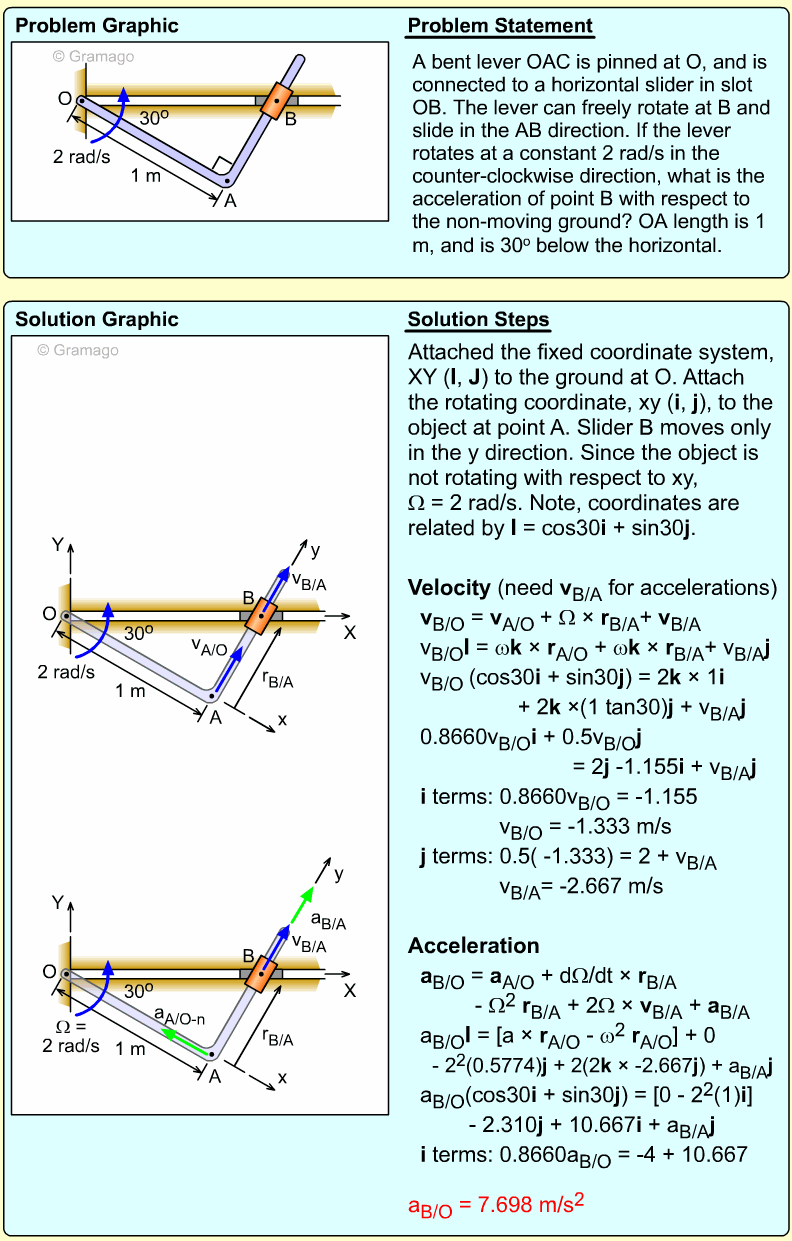
| Example Problem 4 |
||
|
||
| Example Problem 5 |
||
|
||
| Example Problem 6 |
||
|
||
| Example Problem 7 |
||
|
||
| Example Problem 8 |
||
|
||
| Example Problem 9 |
||
|
||