| Ch 5. Fundamental Laws (Differential) | Multimedia Engineering Fluids | ||||||
|
Conservation Mass |
Navier-Stokes and Euler's |
Conservation Energy |
|||||
| Conservation of Energy | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
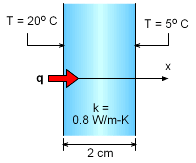
To determine the temperature profile, apply the energy equation to the window glass, The above equation is referred to as the steady-state heat conduction equation without internal heat generation. Since the object of present study is a solid (i.e., window glass), all velocities vanish* (see note). Further, it is assumed that the temperature varies in the x-direction only and the thermal conductivity is a constant. Then energy equation reduces to which can be readily integrated to yield T = c1x + c2 where c1 and c2 are constants to be determined from the temperature boundary conditions (i.e., T = 20 oC = 293 K when x = 0 and T = 5 oC = 278 K when x = 0.02 m). Applying the conditions give c1 = -750 and c2 = 293 |
|
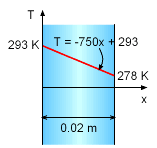 Temperature Profile |
The temperature profile becomes T = -750x + 293 According to Fourier's law of heat conduction, the heat transfer through the window glass per unit area is given by q/A = -k dT/dx = -k (-750) ____________________________ |
|