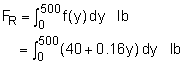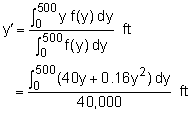| Ch 4. Moments/Equivalent Systems | Multimedia Engineering Statics | ||||||
|
Moment 2-D Scalar |
Moment 3-D Scalar |
Moment 3-D Vector |
Couples and Equiv. System | Distributed Loads, Intro | |||
| Introduction to Distributed Loads | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Integration Method |
||
 Integration Method
|
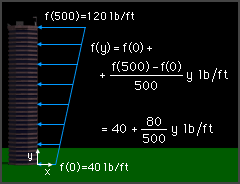
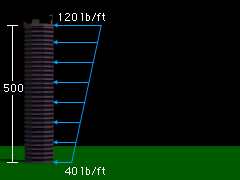
In order to integrate the distributed wind load, determine a function f(y) that describes the wind load. f(y) = 40 + 80/500 y lb/ft The force resultant is given by Its location is given by |
|
| Composite Parts Method |
||
|
|
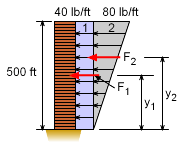
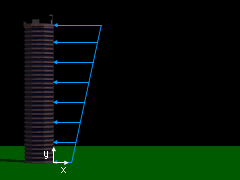
For the composite parts method, first break the wind load
into two parts: a uniform load of 40 lb/ft and a triangular load
of 0 lb/ft at the base and 80 lb/ft at the top of the building.
The force resultant of the uniform load and its location is F1 = 40 (500) = 20,000 lb y1 = 250 ft The force resultant of the triangular load is F2 = 0.5 (80) (500) = 20,000 lb Its location is two-thirds of the distance from the vertex to the peak value y2 = 2/3 (500) = 333.3 ft Nest, combine these two forces into a single force FR located at the position y'. FR = ΣF = F1 + F2 = 40,000 lb Its location is given by Substituting F1, y1, F2, and y2 and simplifying the equation gives y' = 1.166 x 107 / 40,000 |
|