| Ch 3. Fluid Kinematics | Multimedia Engineering Fluids | ||||||
|
Flow Descriptions |
Steady & Unsteady |
Streamlines, Streaklines |
Velocity & Acceleration |
Irrotational Flow |
|||
| Flow Descriptions | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
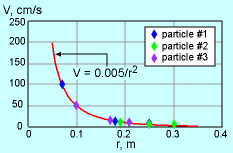
Since it is given that the velocity is inversely proportional to the square of the location r, assume the correlation for velocity has the following form: V = c/r2 where c is a constant which needs to be determined. |
|||||||||||||||||||||||||||||||||||||||||||||||||
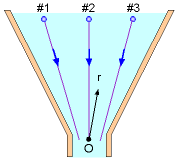
 Schematic of Experiment Set #1 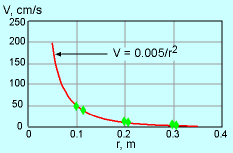 Correlation for Experiment Set #1 |
For experiment set #1, the locations of the measurement points are first determined (using the Pythagorean theorem):
By taking the average of the calculated values for the constant c, it is found that c is 0.00497, which is close to 0.005. The Eulerian viewpoint is used in this experiment since the velocities are measured at fixed locations. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
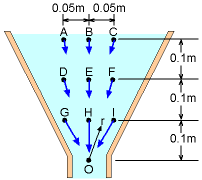
For experiment set #2:
The average value for the constant c is 0.00498, which is again close to 0.005. Since the measurements in set #2 are taken by following individual fluid particles, the flow field is determined using the Lagrangian viewpoint. |
|||||||||||||||||||||||||||||||||||||||||||||||||