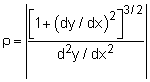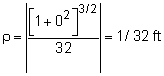| Ch 1. Particle General Motion | Multimedia Engineering Dynamics | ||||||
|
Position, Vel & Accel. |
Accel. vary w/ Time |
Accel. Constant | Rect. Coordinates | Norm/Tang. Coordinates | Polar Coordinates |
Relative Motion |
|
| Curv. Motion: Normal/Tangential | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
 Particle Motion along Path |
Example |
|
|
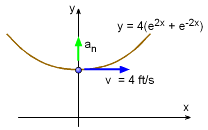
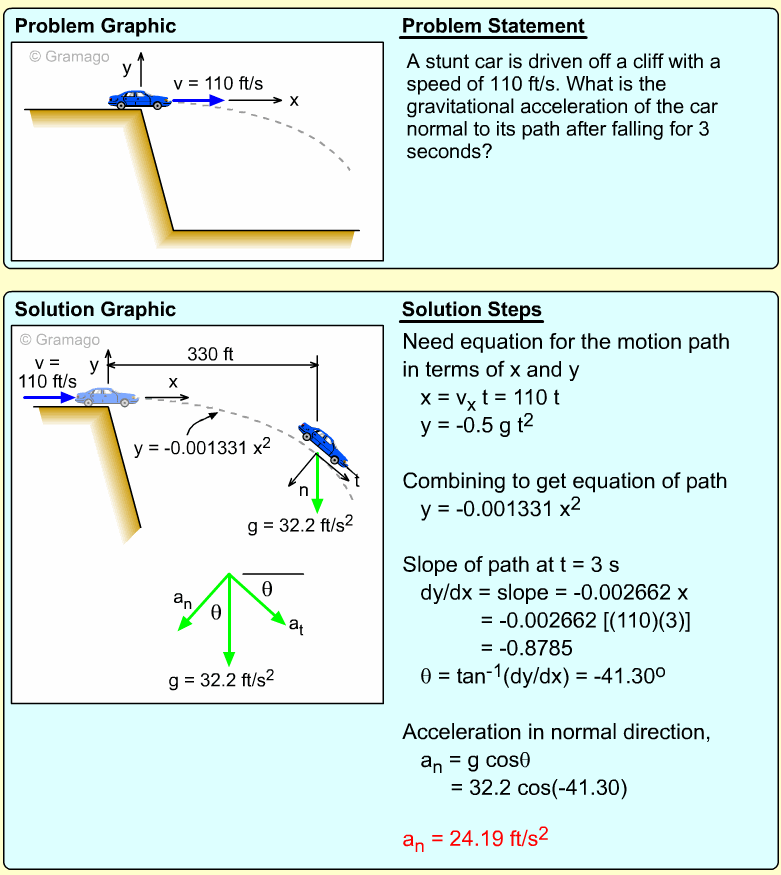
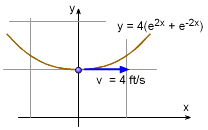
A particle moves along a wire that follows the curve y = 4(e2x + e-2x) at a constant velocity of 4 m/s. What is the normal acceleration of the particle when x = 0?
|
||
| Solution |
||
|
|
Since the velocity is constant, there is no acceleration tangent to its path. However, there is acceleration normal (perpendicular) to the path as given by, an = v2/ρ Need to determine, ρ dy/dx = d[ 4(e2x + e-2x) ] / dx d2y/dx2 = d[ 8(e2x - e-2x ) ] / dx (dy/dx)x=0 = 8(1 - 1) = 0 Substituting back into the acceleration equation, an = 512 ft/s2 |
|
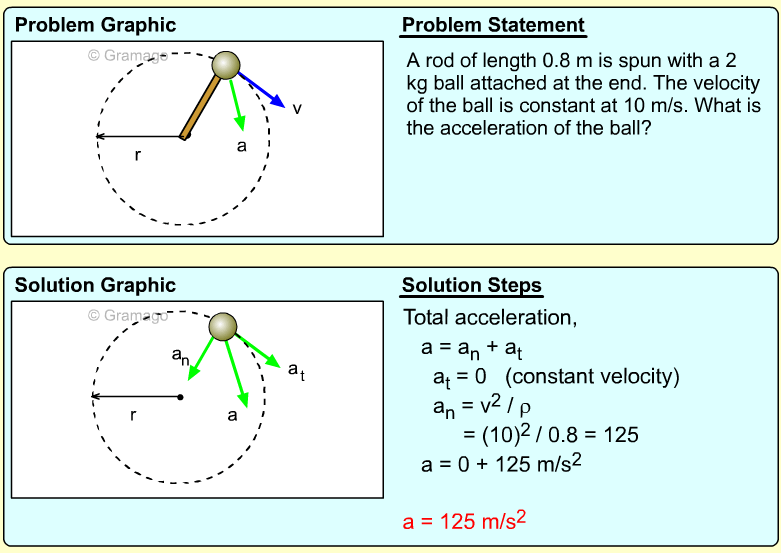
| Example Problem 1 |
||
|
||
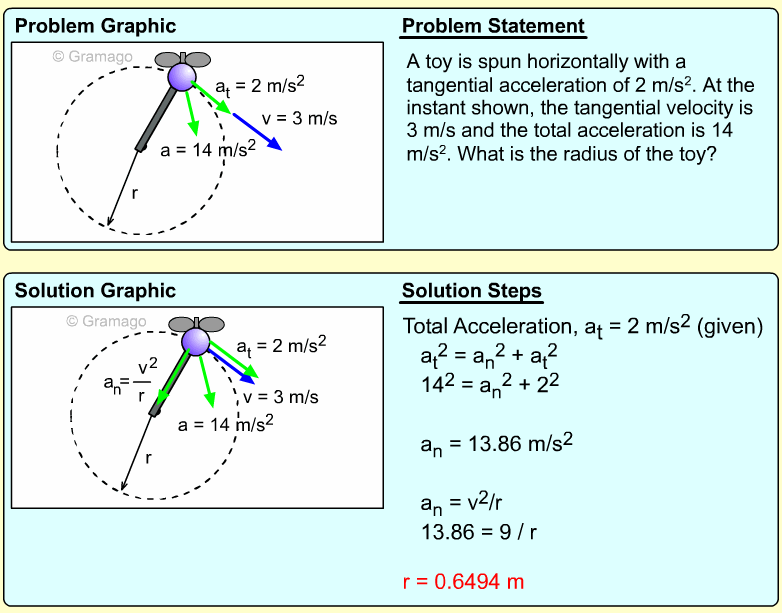
| Example Problem 2 |
||
|
||
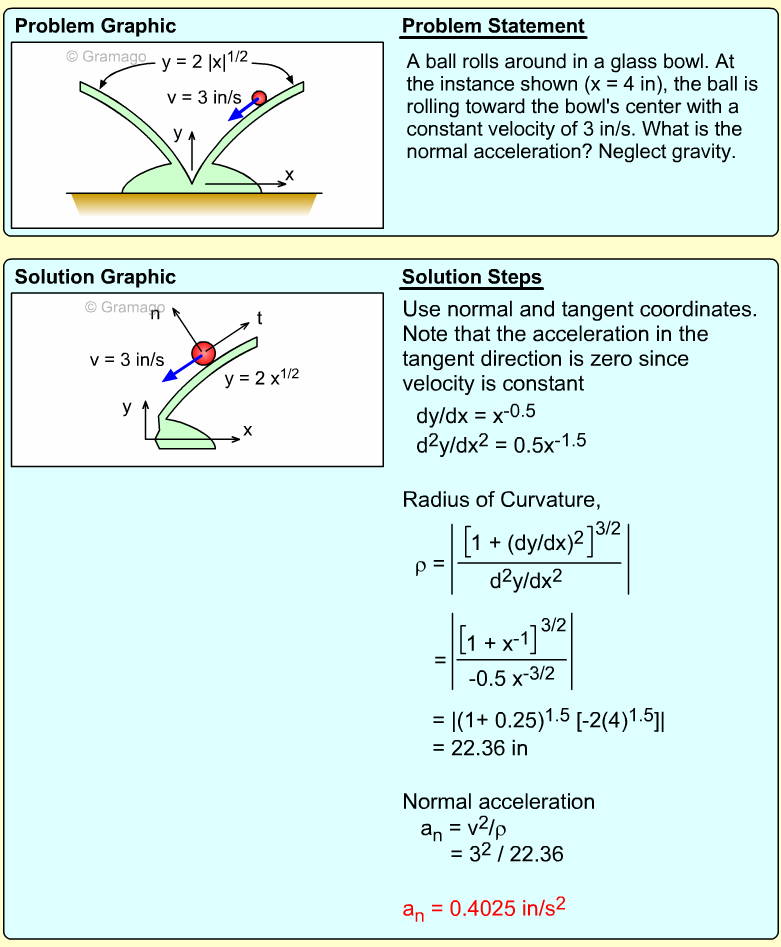
| Example Problem 3 |
||
|
||
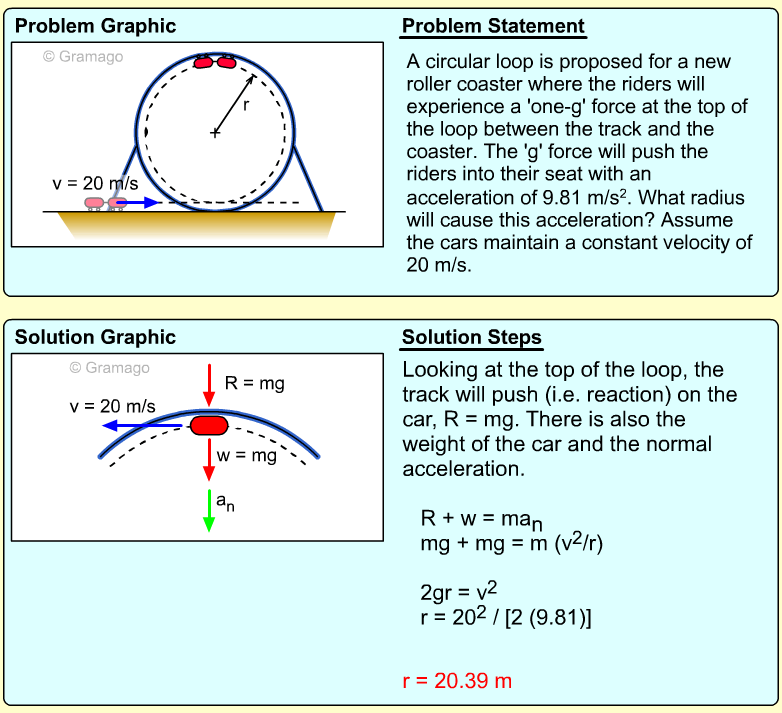
| Example Problem 4 |
||
|
||
| Example Problem 5 |
||
|
||
| Example Problem 6 |
||
|
||
| Example Problem 7 |
||
|
||
| Example Problem 8 |
||
|
||
| Example Problem 9 |
||
|
||
| Example Problem 10 |
||
|
||
| Example Problem 11 |
||
|
||