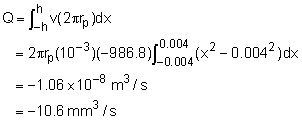Problem Diagram I

Problem Diagram II

From the continuity equation, it can be concluded that the velocity v is a function of x only, i.e, v = v(x).

The Navier-Stokes equations are simplified to

The first and third equations require the pressure to be a function of y only. If the second equation is integrated twice (assumes dp/dy = constant with respect to x), then

Applying the no-slip conditions to obtain the coefficients, and the above equation reduces to

Note that h is one half of the gap width (h = 0.004 mm). Substituting the known values (i.e., μ = 0.38 N-s/m², ρ = 912 kg/m³ and dp/dy = 15 MPa/20 mm), and the velocity profile becomes

       

where the unit of x is mm. The velocity profile of the oil is shown in the figure.

The volumetric flow rate of the leakage can be obtained by integrating the velocity over the cross sectional area as follows:

The negative sign simply indicates that the flow rate is in the negative y direction.

Note: Students are encouraged to calculate the Reynolds number and determine if the assumption of laminar flow is valid.